[10000ダウンロード済み√] (x y)^1/2 formula 247243

Graphs Of Equations

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theoremCommonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written () It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 x) n, and is given by the formula =!!()!For example, the fourth power of 1 x isPut xs and ys together (x2 − 2x) (y2 − 4y) − 4 = 0 Constant on right (x2 − 2x) (y2 − 4y) = 4 Now complete the square for x (take half of the −2, square it, and add to both sides) (x 2 − 2x (−1)2) (y 2 − 4y) = 4 (−1)2 And complete the square for y (take half of the −4, square it, and add to both sides)

(x y)^1/2 formula

(x y)^1/2 formula-Graph y=(x1)(x2) Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus1 Suppose the joint pmf of X and Y isgiven byp(1,1) = 05, p(1,2) = 01, p(2,1) = 01, p(2,2) = 03 Find the pmf of X given Y = 1 Solution pXY=1(1) = p(1,1)/pY (1) = 05/06 = 5/6 pXY=1(2) = p(2,1)/pY (1) = 01/06 = 1/6 2 If X and Y are independent Poisson RVs with respective means λ1 and λ2, find the conditional pmf of X

Transform The Equation X Y 1 0 Into The Normal Form Brainly In

2 cos(x y) cos(x y) sinxcosy= 1 2 sin(x y) sin(x y) SumtoProduct Formulas sinx siny= 2sin xy 2 cos x y 2 sinx siny= 2sin x y 2 cos xy 2 cosx cosy= 2cos xy 2 cos x y 2 cosx cosy= 2sin xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A TheWe previously determined that the conditional distribution of Y given X is 0 1 2 Y 0 1 X 1 / 4 1 / 4 2 / 4 2 / 4 1 / 4 1 / 4 1 1 Therefore, we can use it, that is, h ( y x), and the formula for the conditional mean of Y given X = x to calculate the conditional mean of Y given X = 0Let X and Y be random variables (discrete or continuous!) with means μ X and μ Y The covariance of X and Y, denoted Cov ( X, Y) or σ X Y, is defined as C o v ( X, Y) = σ X Y = E ( X − μ X) ( Y − μ Y) That is, if X and Y are discrete random variables with joint support S, then the covariance of X and Y is C o v ( X, Y) = ∑ ∑

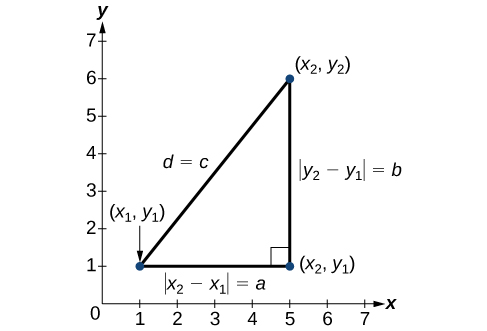
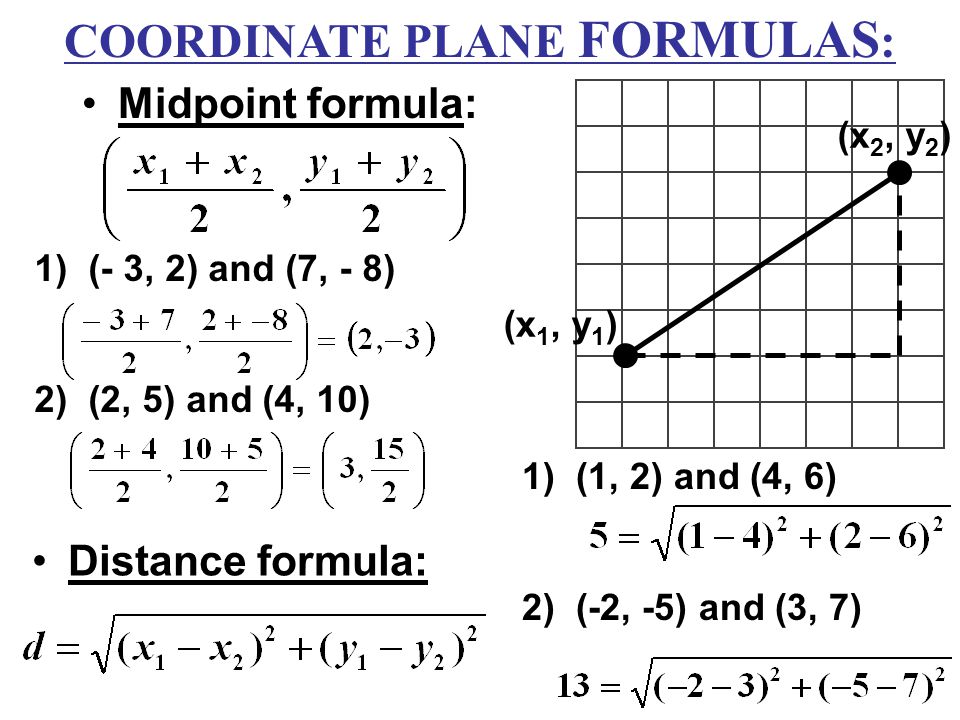
Y ˙ Y Now use the fact that Var(cX) = c2 Var(X) to rewrite that as 1 ˙2 X Var(X) 1 ˙2 Y Var( Y)The slope of a line is calculated using the X and Yaxis Consider two points of a line as F (x 1,y 1) and G(x 2,y 2) Hence, the formula of slope becomes, Slope m = Change in Yaxis/ Change in Xaxis So, m = (y 2 – y 1)/(x 2 – x 1) In other words, the slope of a line increases as it passes from the Y to the Xaxis So, Slope m = Y axis/X axisIf you will complete the square on ##x^2x## you will have ##y = (x\frac 1 2)^2 \frac 1 4## This is a parabola opening up and is therefore not 11 But its vertex is at ##x=\frac 1 2## so the part with ##x>\frac 1 2## is increasing, therefore 11 Solve the completed square equation for ##x## taking the positive root to get ##f^{1}(y)##

(x y)^1/2 formulaのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia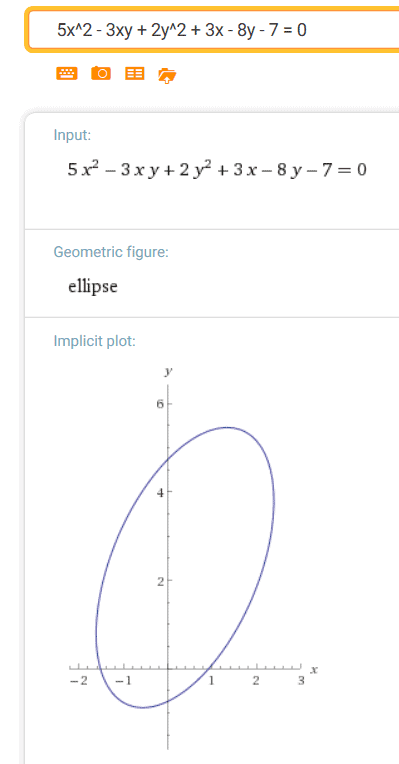
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
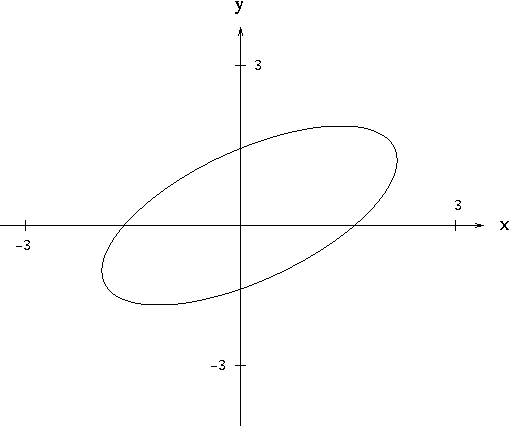Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia	Beta Function Wikipedia	Beta Function Wikipedia
Beta Function Wikipedia

To find the derivative of a ratio, apply the formula D f (x) g(x) = f '(x)g(x) −f (x)g'(x) g2(x) In particular, if f (x) = 1, you have that f '(x) = 0, and the expression becomes D 1 g(x) = −g'(x) g2(x) Since your g(x) is x2, you easily get that g'(x) =2 See answers Advertisement Advertisement sahilverma sahilverma That is the formula of x2y2= (xy)(xy) i don`t know very well refer to