Knowledgebase, relied on by millions of students &آلة حاسبة لمجال دالّة تجد مجال دالّة خطوة بخطوة0 is the domain This consists of all points in the plane except (0;0) This is an open set The range of the function is (1 ;1) Here is a skecth of the level curves f = 1, f = 0, and f = 1

Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com
Find and sketch the domain of the function f(x y)=ln(x^2+y^2-2)
Find and sketch the domain of the function f(x y)=ln(x^2+y^2-2)-Popular Problems Algebra Find the Domain and Range y=x^2 y = x2 y = x 2 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) SetSince et is increasing, f(0;0) = 0 is the smallest possible value for fOn the other hand, by increasing x or y appropriately, we may make the
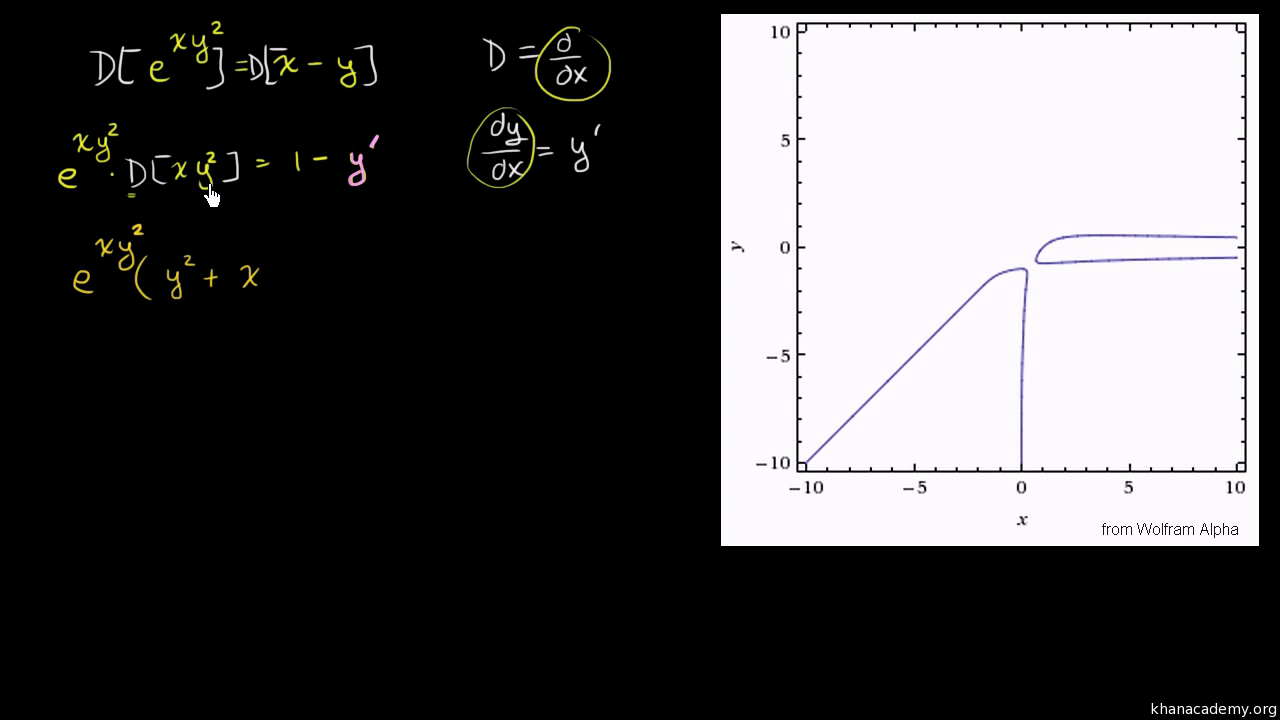


Implicit Differentiation Advanced Example Video Khan Academy
Fresh_42 said In this case you don't have to deal with negative numbers, because the squares are always positive ( − 1) 2 = 1 Therefore only ( x, y) = ( 0, 0) can violate this condition So here x 2 y 2 >View this answer Given the function, f (x,y) = √x2y2−1ln(4−x2−y2) √xy its definition domain if found See full answer below≤ 3 This domain is all ordered pairs (x, y) on the annulus that is centered on the origin, and has inner radius 1 and outer radius √ (3) (b)
This question is most certainly asking about domain!The minimum value of f (x, y) = x 2 y 2 f (x, y) = x 2 y 2 is zero (attained when x = y = 0) x = y = 0) When x = 0, x = 0, the function becomes z = y 2, z = y 2, and when y = 0, y = 0, then the function becomes z = x 2 z = x 2 These are crosssections of the graph, and are parabolas Recall from Introduction to Vectors in Space thatSo f(x;y) is defined only if x2 y2 0 In other words, the domain is x2 y2 0 Note that x2 y2 = (x y)(x y) = 0 Therefore the boundary is the union of two diagonal lines passing through the origin The domain does contain the boundaries Sketch the graph of f(x;y) = e y Because the function f(x;y) does not depends on x, the section of
2) The domain of arcsin (t) is 1, 1 1 ≤ x²Check out a sample textbook solution See solution arrow, ≤ , ≥ * The inequality sign ≤ is entered as the pair of consecutive



Answered 5 F X X 9 2 3 A Find The Bartleby



Solved Multiple Variable Questions Concerning Finding Do Chegg Com
4g This is an annular region in the xyplane (b) f(x;y) = p x p yThe domain of the function f(x,y) = ln(x2 y2−100) f ( x, y) = ln ( x 2 y 2 − 100) is represented by the set of points (x,y) such that the argument of the See full answer belowFind the domain of the function f(x,y)=ln(x^2y^24)!
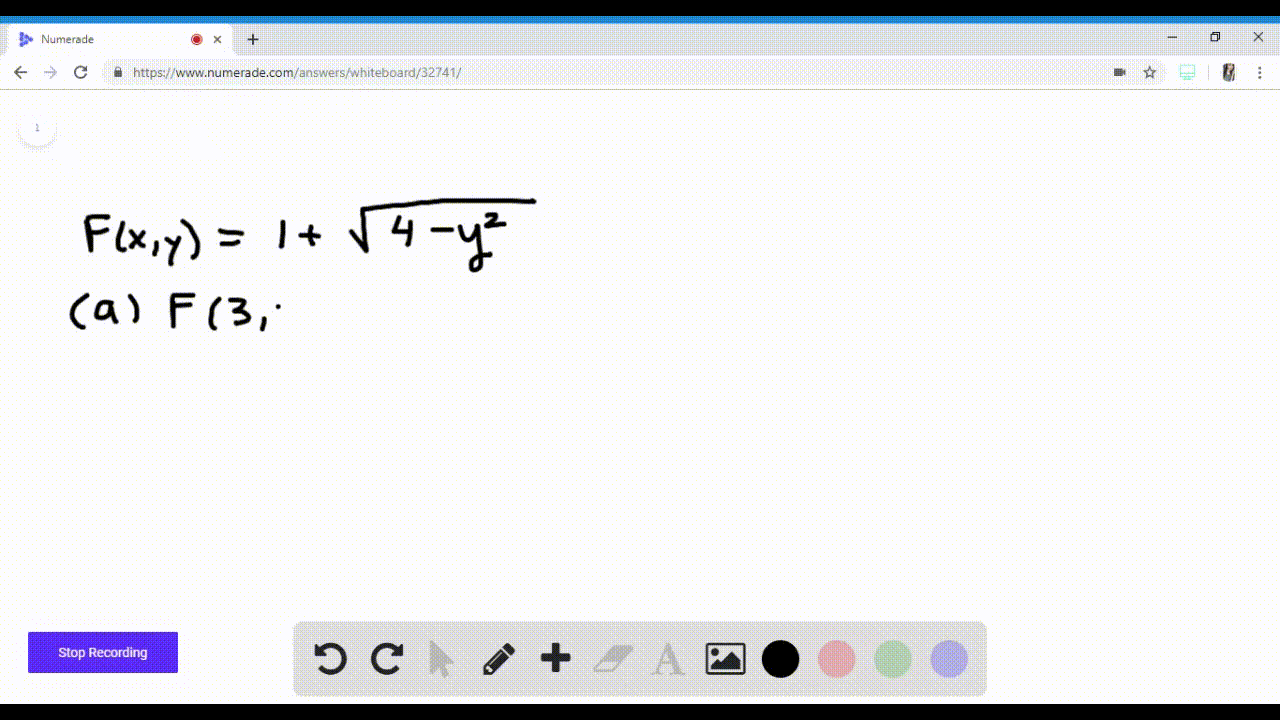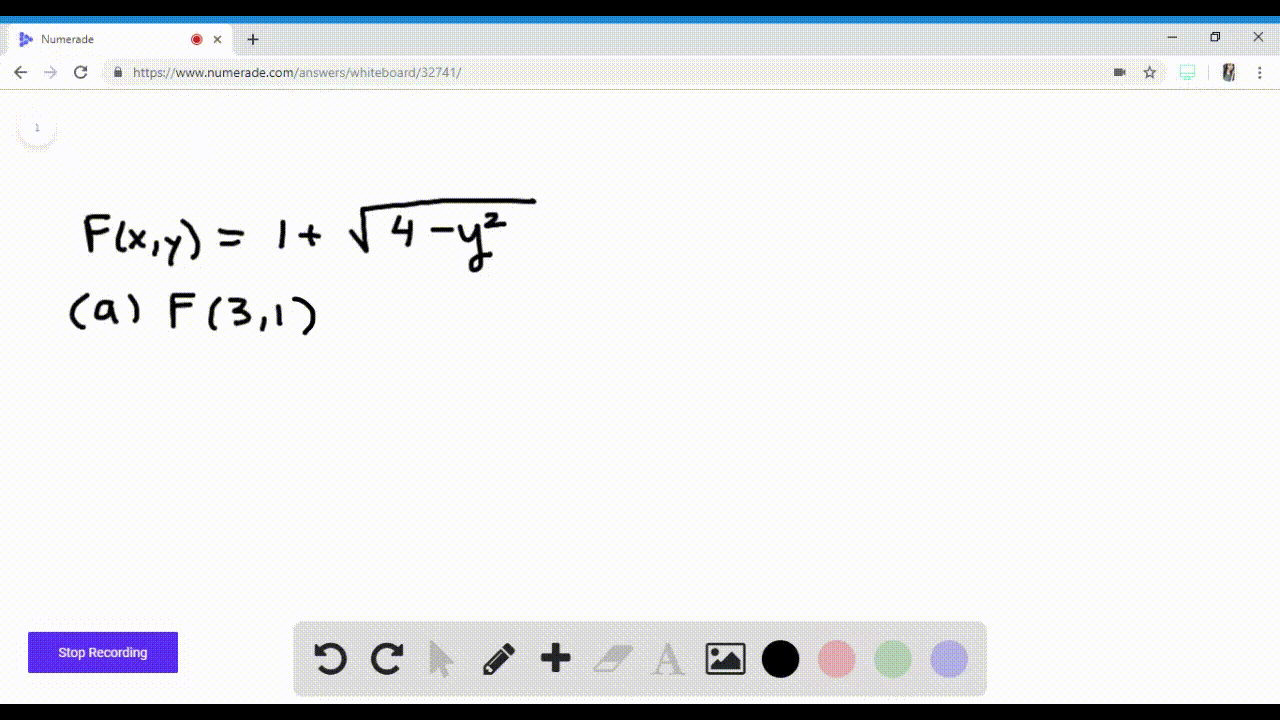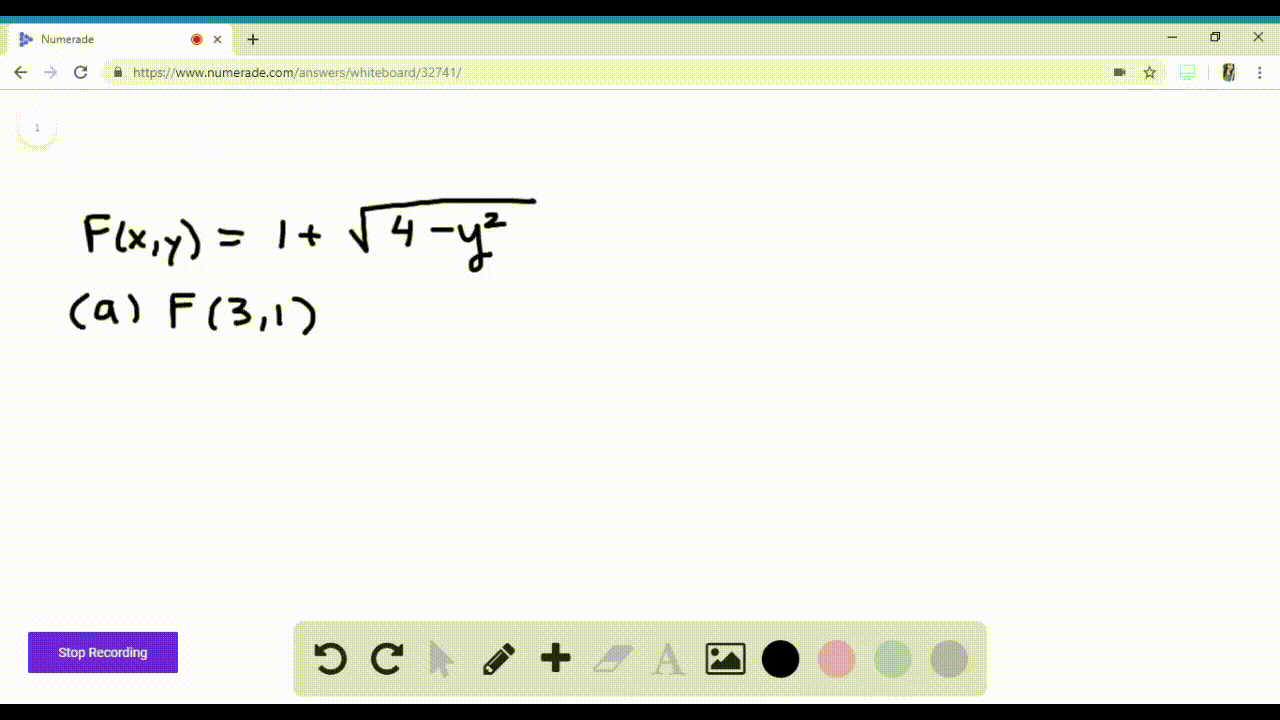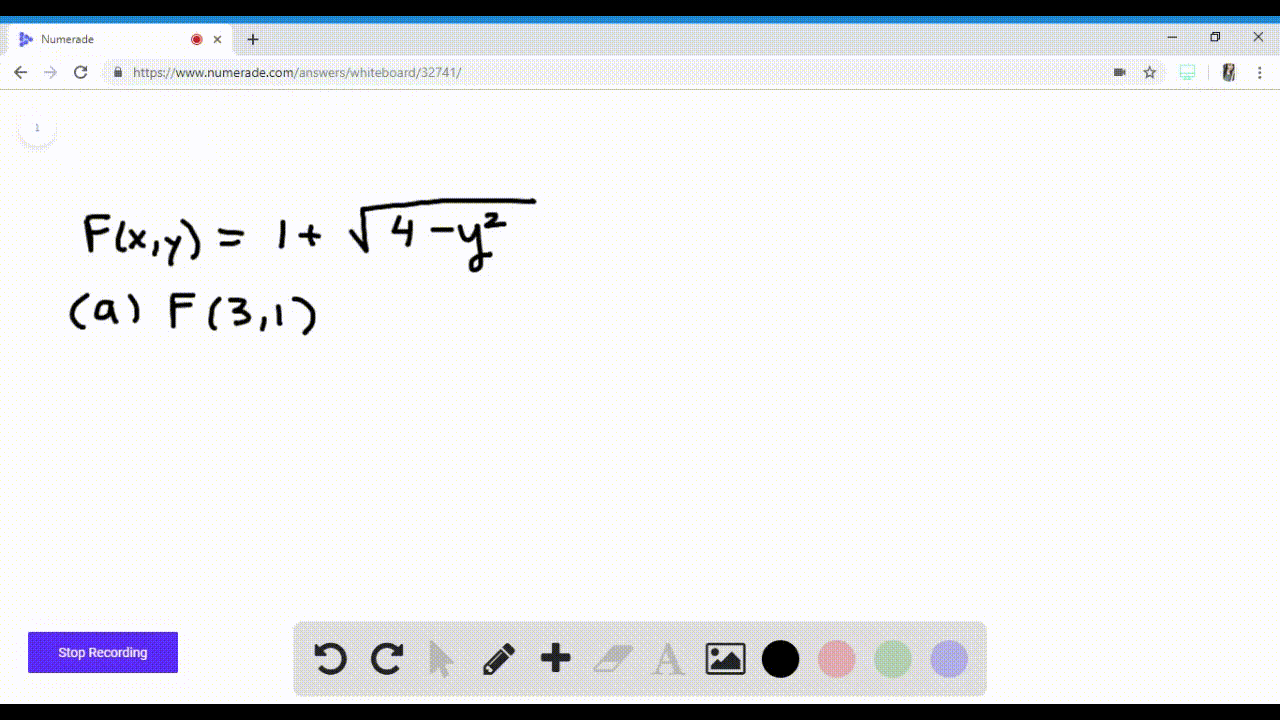


Solved Let F X Y Ln X Y 1 A Evaluate F 1 1


Ejercicios 4 Cvv Holi Matg1002 Studocu
Answers and Replies You are correct The domain is the number plane excluding only the point (0,0) (the 'origin') The equation x 2 y 2 = 0 can be thought of as a degenerate circle whose center is at (0, 0) and whose radius is 0 In other words, the point (0, 0)Safety How worksY(x)=ln(x²) 1 Domain real log requires positive arguments ln(x²) ⇒ x²



How To Find The Domain And Range Of F X Y Ln Xy 2 Youtube



Solved Question 22 Find And Sketch The Domain Of The Func Chegg Com
The area of a function (the main important area) continuously would nicely be chanced on stating restrictthis would nicely be a rational functio and the denominator isn't allowed to be 0So then the restrict is x is different of 0 which make the area {xbelongs to actual variety set x different from 0 for finding out to purchase the diversity there are few procedures you are able to graph the functin it is y= a million/xDomain\f (x)=x^3 domain\f (x)=\ln (x5) domain\f (x)=\frac {1} {x^2} domain\y=\frac {x} {x^26x8} domain\f (x)=\sqrt {x3} domain\f (x)=\cos (2x5) domain\f (x)=\sin (3x) precalculusfunctiondomaincalculator enℂ then the domain is all possible numbers of the set If you start out with ℝ then any real number squared is a positive number, and a square root function is defined fo



Domain And Range Of A Function Algebra Socratic



Solved 1 Find And Sketch The Domain For Each Function A Chegg Com
2 The domain is all values of x x that make the expression defined Interval NotationCompute answers using Wolfram's breakthrough technology &Assuming both f and square root are being defined for either ℝ>ℝ or for ℂ >



Solved What Is The Domain Id Of F Rrett Inter V Cos Chegg Com



Calc 501 1000 By James Bardo Issuu
Find and sketch the domain of the function 22 f ( x , y , z ) = ln(16 − 4 x 2 − 4 y 2 z 2 ) Buy Find launch Calculus Early Transcendentals 8th Edition James Stewart 22 f(x, y, z) = ln(16 − 4x 2 − 4y 2z 2) check_circle Expert Solution Want to see the full answer?Toms calculus Find the domain of ln(x^2y^24) domains of multivariable functions MasterSkills Tutoring Hire A Tutor in NYC References Helpful Books From Amazon Tom's Math Store About Us Mr Circleman Success Stories Payments and CalendarDetermine y grafique el dominio de f(x,y)=ln(9x^29y^2) About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &



Implicit Differentiation Advanced Example Video Khan Academy



Math 148 Exam Iii Practice Problems
The domain of y=f(x) is the range of values of x such that f(x) exists We know that the ln() function does not admit negative arguments, so the domain of f(x) consist of the ranges of x which makes x^24x nonnegative, orDomain= f(x;y) 2R2 x y2 >0g = f(x;y) 2R2 x>y2g While it wasn't necessary to sketch the domain in the xyplane, here is a diagram showing the region Note, the domain is shaded in blue, with an open (dashed) boundary, since ln is unde ned for zero For the range, note that when y= 0, we have f(x;0) = ln(x), and since (x;0) is in our domainThe domain is rather straightforward since all you need is the expression within the root sign to be nonnegative That is, you need 1 x − y2 ≥ 0 or in more simple terms 1 x ≥ y2 So Dom (f(x, y)) = {1 x ≥ y2 ∣ x, y ∈ R} The range is slightly more tricky but not so much



Let F X Be Defined In 0 1 Then The Domain Of Definition
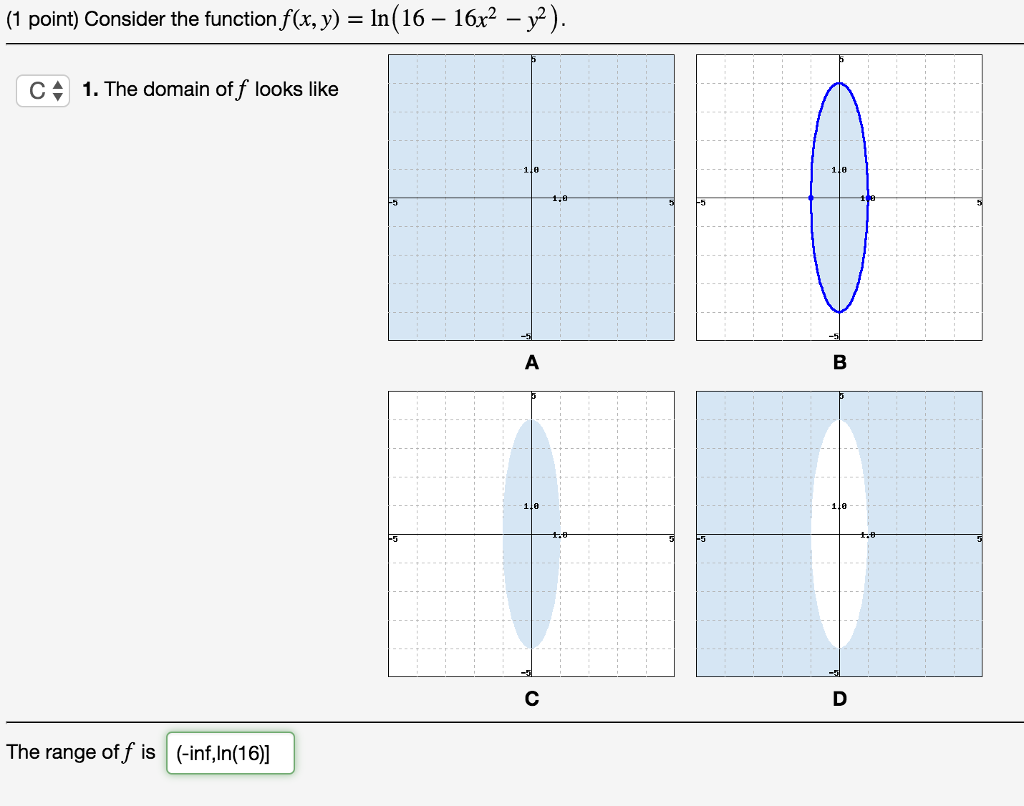


Solved Consider The Function F X Y Ln 16 16x 2 Y Chegg Com
Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;2 Answers2 Active Oldest Votes 1 So the whole bunch x 2 y 2 − 2 is in − 1, 1, you need to think of composition, that is, as long as the range of the function ( x, y) → x 2 y 2 − 2 is the domain of sin ( ⋅), then it goes through Now the domain of the composite map is then { ( x, y) − 1 ≤ x 2 y 2 − 2 ≤ 1 } = { ( x, y) 1 2 ≤ x 2\lim _{x\to 0}(x\ln (x)) \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} stepbystep x^{2}y^{2}=25 en Related Symbolab blog posts Practice, practice, practice Math can be an intimidating subject Each new topic we learn has symbols and problems we have never seen



Chap14 Et Student Solutions Contour Line Curve



Domain And Derivative Of X 2 Ln 1 X 2 Youtube
Tangent plane to x^2 y^2 at (x,y)=(1,2) x^2 y^2 >Professionals For math, science, nutrition, history2 ≤ 1 1 ≤ x²



Assignment Previewer Department Of Mathematics Ccny Pages 1 22 Flip Pdf Download Fliphtml5



How To Draw The Domain Of A Three Variable Function Mathematics Stack Exchange
Let f(x,y)=1/(x^2y^2) for (x,y)\neq 0 Determine whether f is integrable over U0 and over \mathbb{R}^2\bar{U};Show in 2 ways that the function ln(x^2y^2) is harmonic in every domain that does not contain the origin My problem with this quesiton is firstly, I don't know two ways, because normally I would do CauchyRiemann equations but there is no real/imaginary numbers so I don't know what is u(x,y) and what is v(x,y) As a function I know that if I differentiate in terms of x I get 2x/(x^2y^2Boundary is always given by x= yand the right boundary is always given by the larger value of x for which y= 4x x2 Using the quadratic formula for the equivalent equation x2 4x y= 0, this value is x= 2 p 4 y, so we have ZZ D f(x;y)dA= Z y=3 y=0 Z x=2 p 4 y x=y xdxdy = 1 2 Z y=3 y=0 (2 p 4 y)2 y2 dy = 175 12 8



Multivariable Calculus Finding And Sketching The Domain Youtube


What Is The Domain And Range Of 1 X 3 Quora
0 (Tax)/(Day) Buslaev's criteria for continued fraction convergence0 is equivalent to ( x, y) ≠ ( 0, 0) As soon as one is unequal zero, the point is with in the domainF(x, y) = ln( x^2−5 xy^27 1) The domain of f(x, y) can be expressed as a set { (x, y) rel } where rel is a relation involving x and y Enter a suitable relation rel below Notes * A relation is either an equation or an inequality, essentially something of form lhs op rhs where op can be any one of =, <
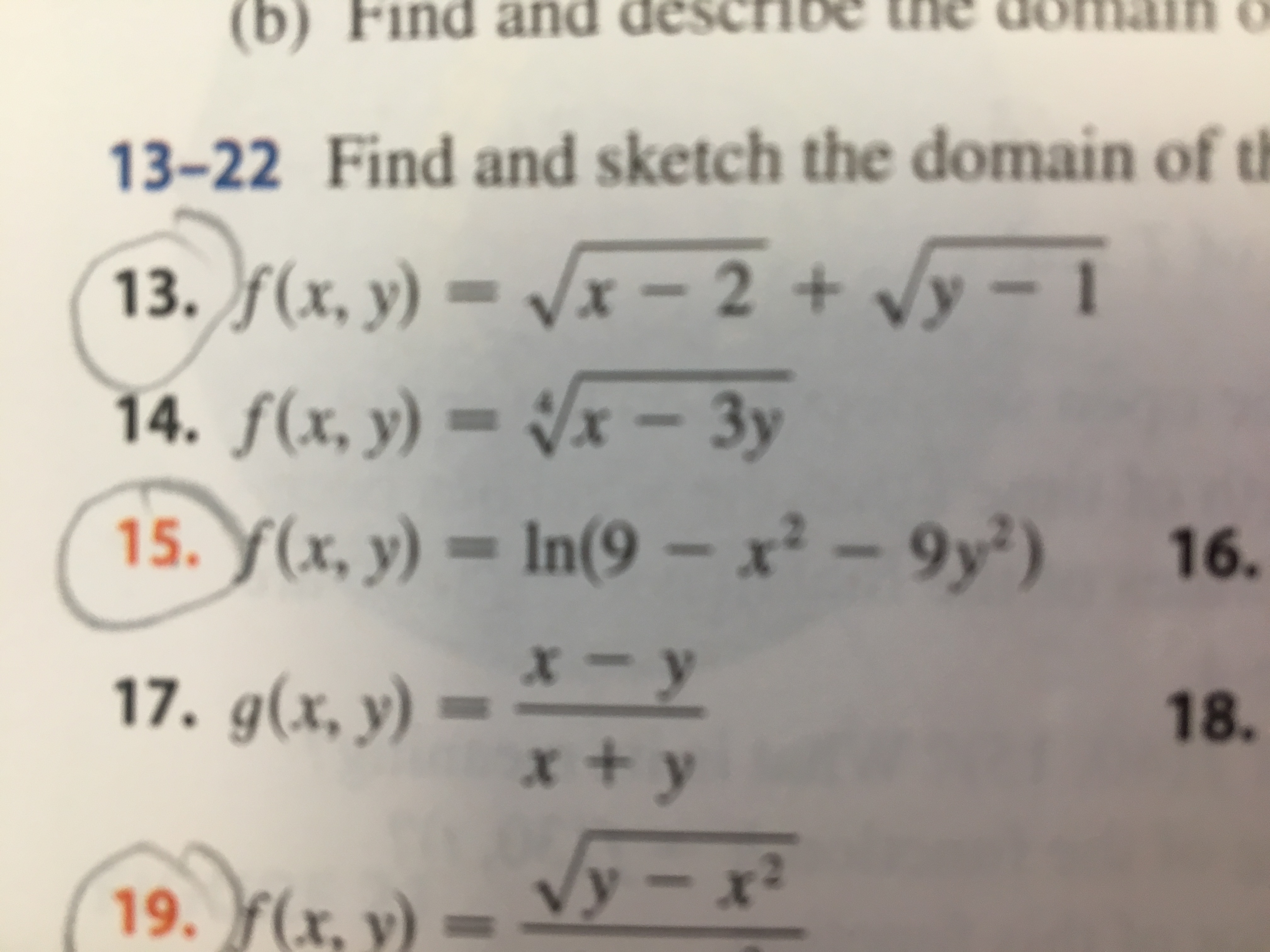


Answered B Find And Describe The Do 13 22 Find Bartleby
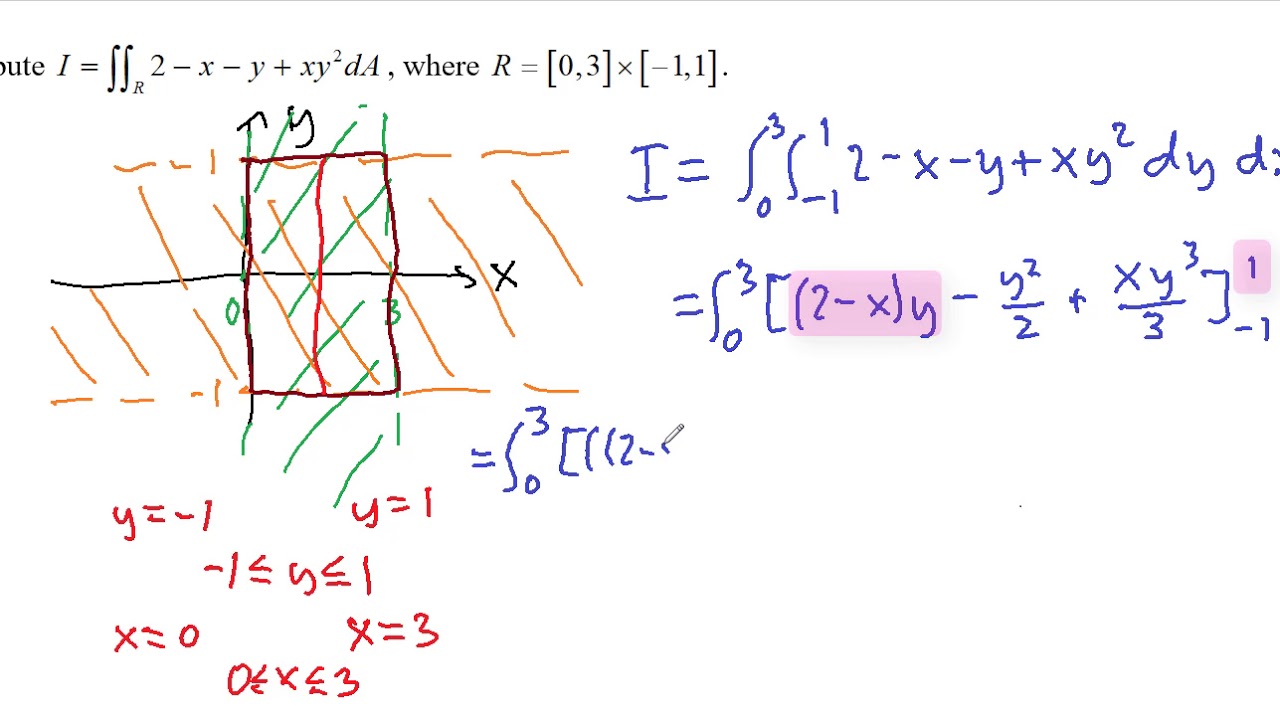


Double Integrals Volume And Average Value
A f x y ln x 2 y 2 9 b f x y x 1 y 2 y x y x 2 4 Consider the function f x y p from MH 1811 at Nanyang Technological University0 ⇒ None solution Domain=ØYou need to figure out for what values x, y, and z is f(x,y,z) not defined I copied the question as it was written, but since we have z



Ln X 2



Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube
Domain of f(x,y) = log(1(x^2y^2)) Extended Keyboard;1) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withJoin a Numerade study group on Discord



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com



Answered 12 Let G X Y Z X Y Z 10 X Y Bartleby
Then y cannot be less than x2 If f(x;y) = 1 xy then xy cannot be zero The domain of a function is assumed to be the largest set for which the de ning rule generates real numbers, unless the domain is otherwise speci ed explicitly The range consists of the set of output values for the dependent variableMathf (x, y)=\ln {(xy)}/math Does not exists logarithm of a nonpositive number So, the domain is mathxy>0/math The mathxy/mathplane has four quadrantsIn the definition of function f(x)A → B it is required that the two sets A and B are different from the empty set So y (x) is not a function



6 Ways To Find The Domain Of A Function Wikihow



Assignment Previewer Department Of Mathematics Ccny Pages 1 22 Flip Pdf Download Fliphtml5
Find and sketch the domain for each function a f x y ln x 2 y 2 9 SOLUTION Note from MH 1811 at Nanyang Technological UniversityAnswer to Find and sketch the domain of the functionf(x, y) = ln(x2 y2 − 2)1703How to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support



Solutions To Assignment 7



Domain Of A Multivariable Function Kristakingmath Youtube
Section 141√ x2 y2In addition, et has domain all reals, so √ x2 y2 may take on any value we wish So the domain of f is the entire xy plane To determine the range, notice that the smallest value for √ x2 y2 is 0 (by choosing x = y = 0);Queries Question from anu, a student the question says we have to find the points in the plane where the function is continuous f (x,y)=ln (x^2y^2) here we aren't given a particular point (x,y) where we have to check a function's continuity what is to be done if we have to check continuity over the whole domain of the function?(b) f(x,y) = 2x2 xy2 −2, D= {(x,y) ∈ R2;x2 y2 64} Solution (a) Calculating the partial derivatives gives f x = y 2 √ x − 1, f y = √ x−2y 6 Finding critical points f x = 0, f y = 0 =⇒ (x,y) = (4,4) Note that (4,4) ∈ Dand that f(4,4) = 12 The boundary of Dconsists of four line segments



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com



Solved 1 12 Marks Let F X Y In X2 Y2 They Are Not Chegg Com
0 x 2 >We have to find the domain of the function y= ln (x^2 3x 2) Now domain refers to all the values of x for which y exists Here y will exist for all values of x that allow x^2 3x 2 to beF(x;y) = p y x2;



Chapter 7 Calculus Of Several Variables



Sketching The Domain And Level Curves Of A Multivariable Function Of F X Y Mathematics Stack Exchange
Best Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it(Empty set) 2 y(x) is a function?Think it this way \ln(e^{f(x)}) defines the exponent such that if you take e to the power of that exponent, will equal to f(x) So, what power does e need to be raised to for it to equal to e



Contour Map Of F X Y 1 X 2 Y 2 Youtube



Derivative Ln X Page 1 Line 17qq Com
Favorite Answer (a) f (x, y) = arcsin (x²(c) f(x;y) = ln(x2 y2) Solution x2 y2 >Find the domain and range of the function f(x, y)=\sqrt{4x^{2}y^{2}} Join our Discord to get your questions answered by experts, meet other students and be entered to win a PS5!



Domain Of F X Log 1 X Sqrt X 2 1 Youtube


1 Determine The Domain For The Following Function And Draw The Graph In Xy Plane F X Y Ln X Y 2 8 Marks 2 For Z F X Y E4x2 9y14m Course Hero
The set D is called the domain of f and ff(x;y)j(x;y) 2Dgis called the range of f Example Find and sketch the domain of the given functions (a) f(x;y) = p x2 y2 1 ln(4 x2 y2) The function is de ned for x 2 y 1 0 and 4 x2 y2 0 The domain is D = f(x;y) 2R2j1 x2 y2 <Domain is given by #x^2 1# >0 That means all real values of x, that is, it would be #RR# For range, exchange x and y in #y= ln (x^21)# and find the domain Accordingly, #x= ln(y^2 1)# #y^2= e^x1# The domain of this function is all #x>= 0# that means all real numbers #>=# =0 Hence the range of given function would be all Real numbers #>=0#0 Add 2 2 to both sides of the inequality x >
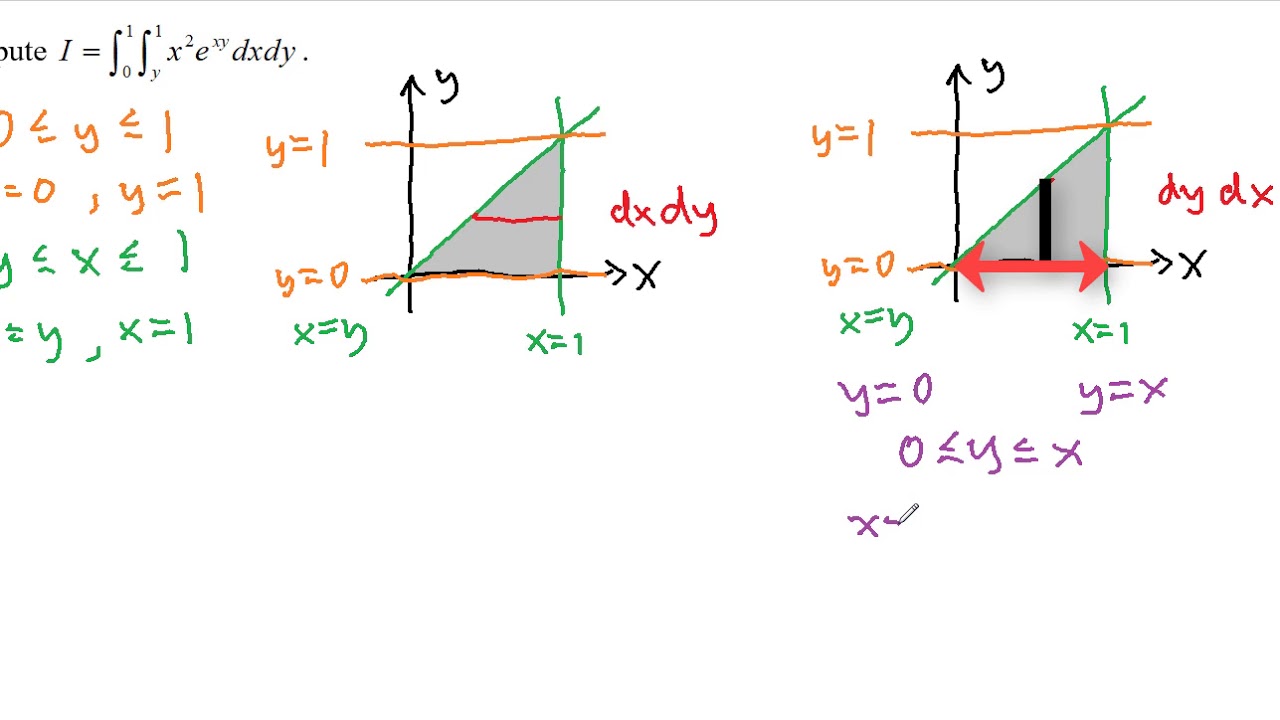


Double Integrals Volume And Average Value



Derivative Of F X Sqrt Ln X Math Videos Calculus Chain Rule
Domain for y=ln(x^2) is x in R but x!=0, in other words (oo,0)uu(0,oo) and range is (oo,oo) We cannot have logarithm of a number less than or equal to zero As x^2 is always positive, only value not permissible is 00309Find and sketch the domain of the function f(x, y) = \ln (9 x^2 9y^2) Video Transcript All right, So let's find the domain And we know that whatever is inside, the argument of a one has to be bigger than zeroF (x) = ln (x − 2) f ( x) = ln ( x 2) Set the argument in ln(x−2) ln ( x 2) greater than 0 0 to find where the expression is defined x−2 >



Functions Inverses Ppt Download
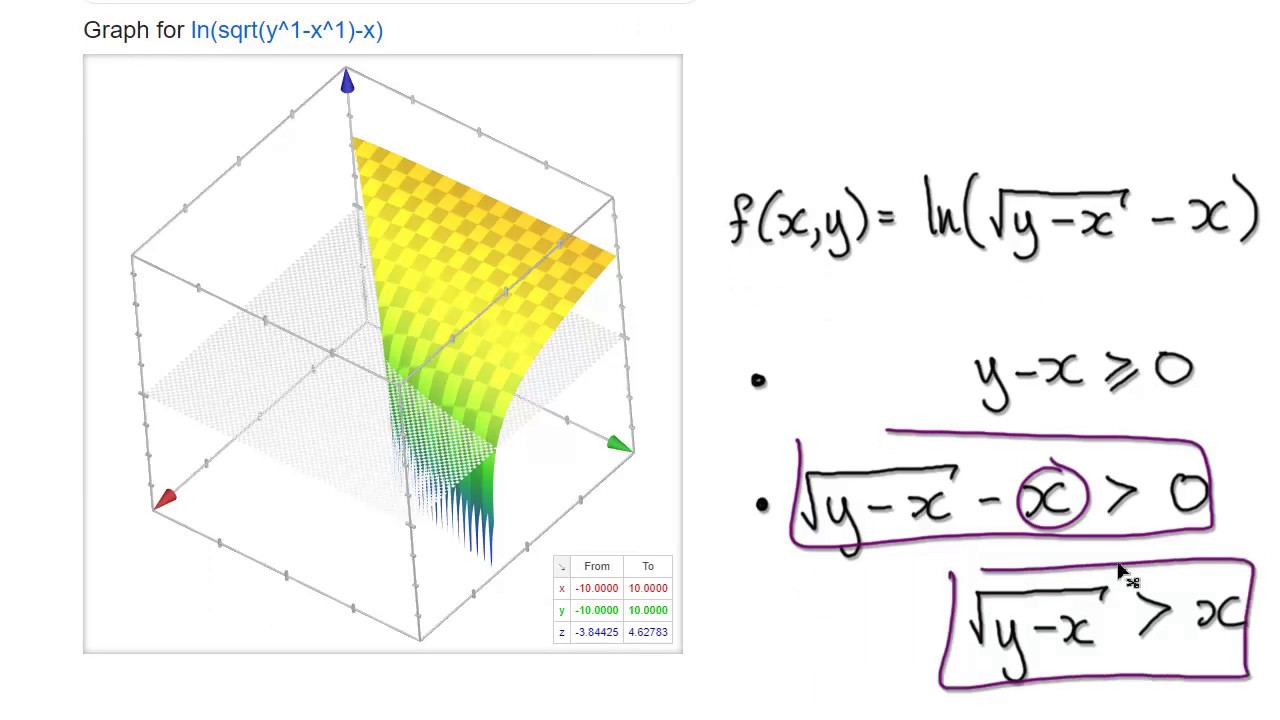


Video 3107 F X Y Ln Sqrt Y X X Multivariable Functions Domain Youtube
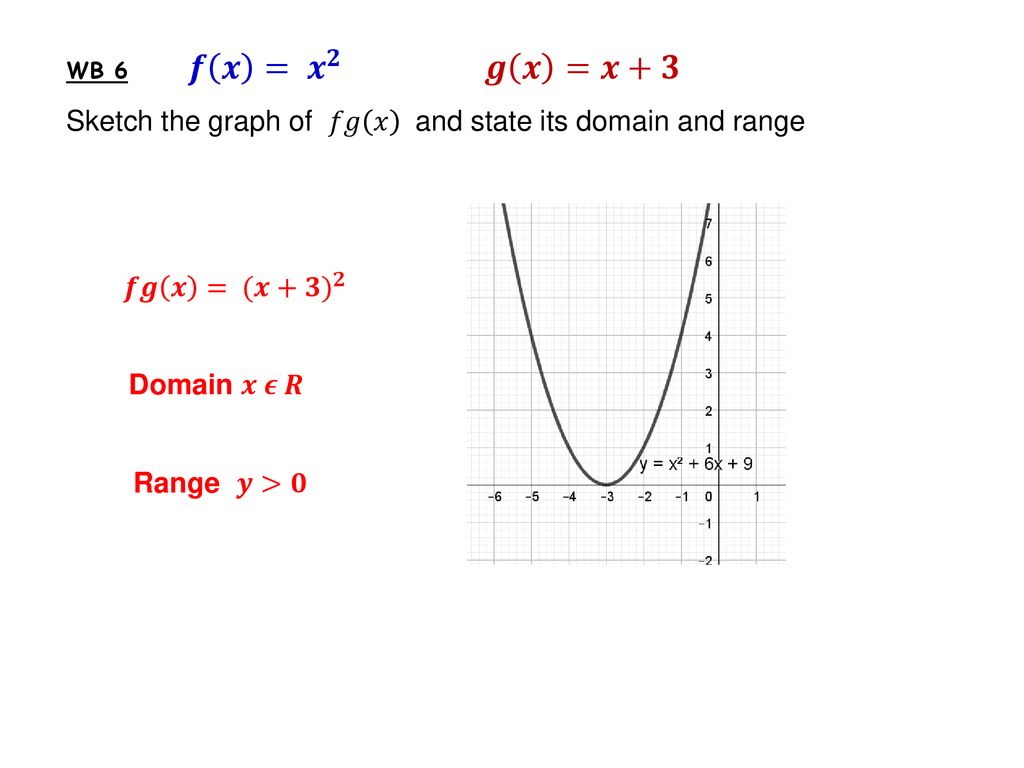


Functions Composite Ppt Download
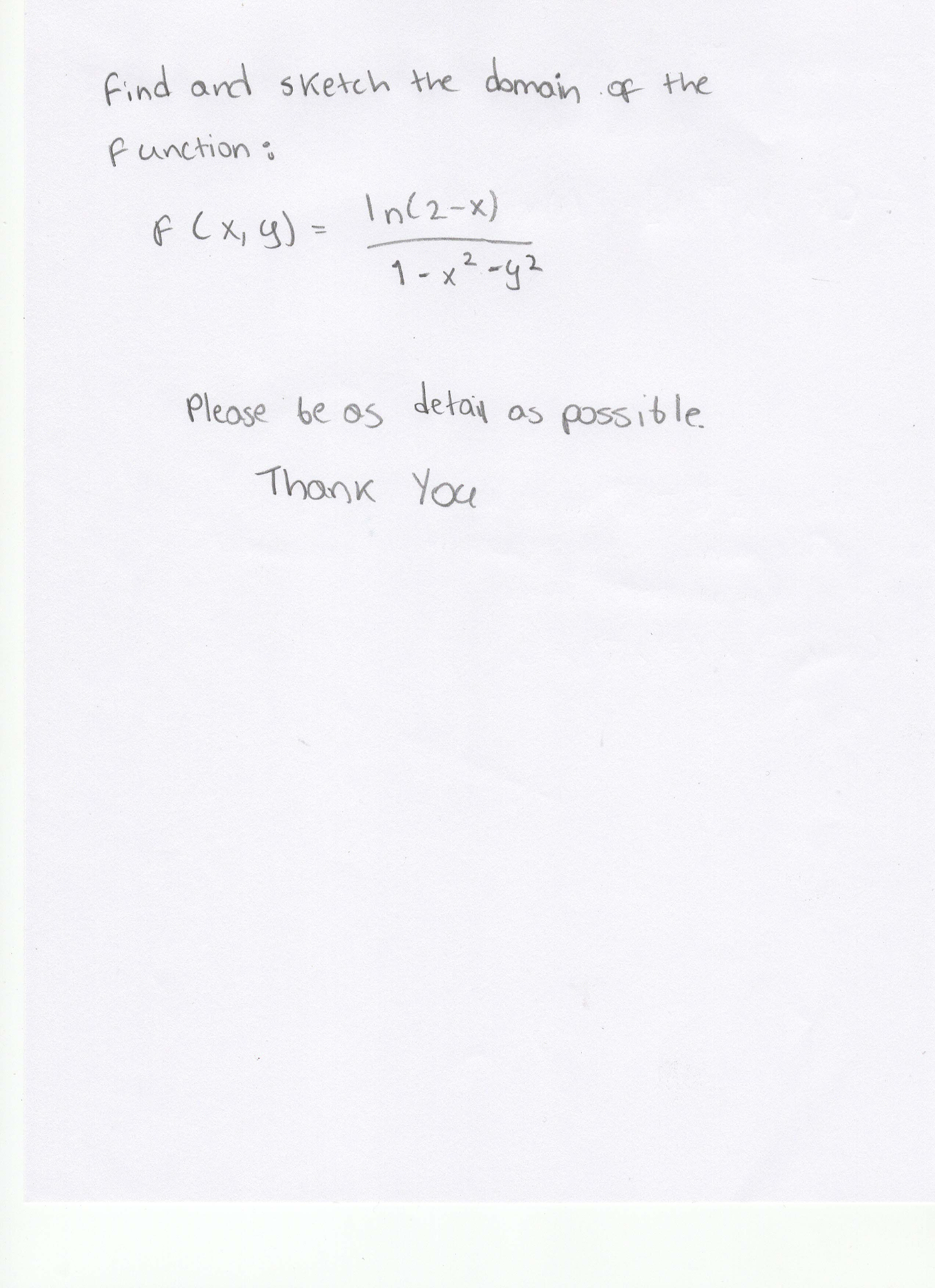


Solved Find And Sketch The Domain Of The Function F X Y Chegg Com



F X Ln X 4 Domain Range Graph And Its Inverse Youtube



Document



Absolute Minima Maxima Entire Domain Video Khan Academy



Functions Inverses Ppt Download



How To Graph The Domain Of Question 11 Calculus



Implicit Differentiation Advanced Example Video Khan Academy


Solved Consider The Function Below F X Y Ln X Y Chegg Com



0 件のコメント:
コメントを投稿